lw_dist2d_arc_arc()

int lw_dist2d_arc_arc	(	const POINT2D *	A1,
		const POINT2D *	A2,
		const POINT2D *	A3,
		const POINT2D *	B1,
		const POINT2D *	B2,
		const POINT2D *	B3,
		DISTPTS *	dl
	)

Definition at line 1575 of file measures.c.

{
        POINT2D CA, CB;               /* Center points of arcs A and B */
        double radius_A, radius_B, d; /* Radii of arcs A and B */
        POINT2D D;                    /* Mid-point between the centers CA and CB */
        int pt_in_arc_A, pt_in_arc_B; /* Test whether potential intersection point is within the arc */
 
        if (dl->mode != DIST_MIN)
                lwerror("lw_dist2d_arc_arc only supports mindistance");
 
        /* TODO: Handle case where arc is closed circle (A1 = A3) */
 
        /* What if one or both of our "arcs" is actually a point? */
        if (lw_arc_is_pt(B1, B2, B3) && lw_arc_is_pt(A1, A2, A3))
                return lw_dist2d_pt_pt(B1, A1, dl);
        else if (lw_arc_is_pt(B1, B2, B3))
                return lw_dist2d_pt_arc(B1, A1, A2, A3, dl);
        else if (lw_arc_is_pt(A1, A2, A3))
                return lw_dist2d_pt_arc(A1, B1, B2, B3, dl);
 
        /* Calculate centers and radii of circles. */
        radius_A = lw_arc_center(A1, A2, A3, &CA);
        radius_B = lw_arc_center(B1, B2, B3, &CB);
 
        /* Two co-linear arcs?!? That's two segments. */
        if (radius_A < 0 && radius_B < 0)
                return lw_dist2d_seg_seg(A1, A3, B1, B3, dl);
 
        /* A is co-linear, delegate to lw_dist_seg_arc here. */
        if (radius_A < 0)
                return lw_dist2d_seg_arc(A1, A3, B1, B2, B3, dl);
 
        /* B is co-linear, delegate to lw_dist_seg_arc here. */
        if (radius_B < 0)
                return lw_dist2d_seg_arc(B1, B3, A1, A2, A3, dl);
 
        /* Center-center distance */
        d = distance2d_pt_pt(&CA, &CB);
 
        /* Concentric arcs */
        if (FP_EQUALS(d, 0.0))
                return lw_dist2d_arc_arc_concentric(A1, A2, A3, radius_A, B1, B2, B3, radius_B, &CA, dl);
 
        /* Make sure that arc "A" has the bigger radius */
        if (radius_B > radius_A)
        {
                const POINT2D *tmp;
                POINT2D TP; /* Temporary point P */
                double td;
                tmp = B1;
                B1 = A1;
                A1 = tmp;
                tmp = B2;
                B2 = A2;
                A2 = tmp;
                tmp = B3;
                B3 = A3;
                A3 = tmp;
                TP = CB;
                CB = CA;
                CA = TP;
                td = radius_B;
                radius_B = radius_A;
                radius_A = td;
        }
 
        /* Circles touch at a point. Is that point within the arcs? */
        if (d == (radius_A + radius_B))
        {
                D.x = CA.x + (CB.x - CA.x) * radius_A / d;
                D.y = CA.y + (CB.y - CA.y) * radius_A / d;
 
                pt_in_arc_A = lw_pt_in_arc(&D, A1, A2, A3);
                pt_in_arc_B = lw_pt_in_arc(&D, B1, B2, B3);
 
                /* Arcs do touch at D, return it */
                if (pt_in_arc_A && pt_in_arc_B)
                {
                        dl->distance = 0.0;
                        dl->p1 = D;
                        dl->p2 = D;
                        return LW_TRUE;
                }
        }
        /* Disjoint or contained circles don't intersect. Closest point may be on */
        /* the line joining CA to CB. */
        else if (d > (radius_A + radius_B) /* Disjoint */ || d < (radius_A - radius_B) /* Contained */)
        {
                POINT2D XA, XB; /* Points where the line from CA to CB cross their circle bounds */
 
                /* Calculate hypothetical nearest points, the places on the */
                /* two circles where the center-center line crosses. If both */
                /* arcs contain their hypothetical points, that's the crossing distance */
                XA.x = CA.x + (CB.x - CA.x) * radius_A / d;
                XA.y = CA.y + (CB.y - CA.y) * radius_A / d;
                XB.x = CB.x + (CA.x - CB.x) * radius_B / d;
                XB.y = CB.y + (CA.y - CB.y) * radius_B / d;
 
                pt_in_arc_A = lw_pt_in_arc(&XA, A1, A2, A3);
                pt_in_arc_B = lw_pt_in_arc(&XB, B1, B2, B3);
 
                /* If the nearest points are both within the arcs, that's our answer */
                /* the shortest distance is at the nearest points */
                if (pt_in_arc_A && pt_in_arc_B)
                {
                        return lw_dist2d_pt_pt(&XA, &XB, dl);
                }
        }
        /* Circles cross at two points, are either of those points in both arcs? */
        /* http://paulbourke.net/geometry/2circle/ */
        else if (d < (radius_A + radius_B))
        {
                POINT2D E, F; /* Points where circle(A) and circle(B) cross */
                /* Distance from CA to D */
                double a = (radius_A * radius_A - radius_B * radius_B + d * d) / (2 * d);
                /* Distance from D to E or F */
                double h = sqrt(radius_A * radius_A - a * a);
 
                /* Location of D */
                D.x = CA.x + (CB.x - CA.x) * a / d;
                D.y = CA.y + (CB.y - CA.y) * a / d;
 
                /* Start from D and project h units perpendicular to CA-D to get E */
                E.x = D.x + (D.y - CA.y) * h / a;
                E.y = D.y + (D.x - CA.x) * h / a;
 
                /* Crossing point E contained in arcs? */
                pt_in_arc_A = lw_pt_in_arc(&E, A1, A2, A3);
                pt_in_arc_B = lw_pt_in_arc(&E, B1, B2, B3);
 
                if (pt_in_arc_A && pt_in_arc_B)
                {
                        dl->p1 = dl->p2 = E;
                        dl->distance = 0.0;
                        return LW_TRUE;
                }
 
                /* Start from D and project h units perpendicular to CA-D to get F */
                F.x = D.x - (D.y - CA.y) * h / a;
                F.y = D.y - (D.x - CA.x) * h / a;
 
                /* Crossing point F contained in arcs? */
                pt_in_arc_A = lw_pt_in_arc(&F, A1, A2, A3);
                pt_in_arc_B = lw_pt_in_arc(&F, B1, B2, B3);
 
                if (pt_in_arc_A && pt_in_arc_B)
                {
                        dl->p1 = dl->p2 = F;
                        dl->distance = 0.0;
                        return LW_TRUE;
                }
        }
        else
        {
                lwerror("lw_dist2d_arc_arc: arcs neither touch, intersect nor are disjoint! INCONCEIVABLE!");
                return LW_FALSE;
        }
 
        /* Closest point is in the arc A, but not in the arc B, so */
        /* one of the B end points must be the closest. */
        if (pt_in_arc_A && !pt_in_arc_B)
        {
                lw_dist2d_pt_arc(B1, A1, A2, A3, dl);
                lw_dist2d_pt_arc(B3, A1, A2, A3, dl);
                return LW_TRUE;
        }
        /* Closest point is in the arc B, but not in the arc A, so */
        /* one of the A end points must be the closest. */
        else if (pt_in_arc_B && !pt_in_arc_A)
        {
                lw_dist2d_pt_arc(A1, B1, B2, B3, dl);
                lw_dist2d_pt_arc(A3, B1, B2, B3, dl);
                return LW_TRUE;
        }
        /* Finally, one of the end-point to end-point combos is the closest. */
        else
        {
                lw_dist2d_pt_pt(A1, B1, dl);
                lw_dist2d_pt_pt(A1, B3, dl);
                lw_dist2d_pt_pt(A3, B1, dl);
                lw_dist2d_pt_pt(A3, B3, dl);
                return LW_TRUE;
        }
 
        return LW_TRUE;
}

References DIST_MIN, DISTPTS::distance, distance2d_pt_pt(), FP_EQUALS, lw_arc_center(), lw_arc_is_pt(), lw_dist2d_arc_arc_concentric(), lw_dist2d_pt_arc(), lw_dist2d_pt_pt(), lw_dist2d_seg_arc(), lw_dist2d_seg_seg(), LW_FALSE, lw_pt_in_arc(), LW_TRUE, lwerror(), DISTPTS::mode, DISTPTS::p1, DISTPTS::p2, POINT2D::x, and POINT2D::y.

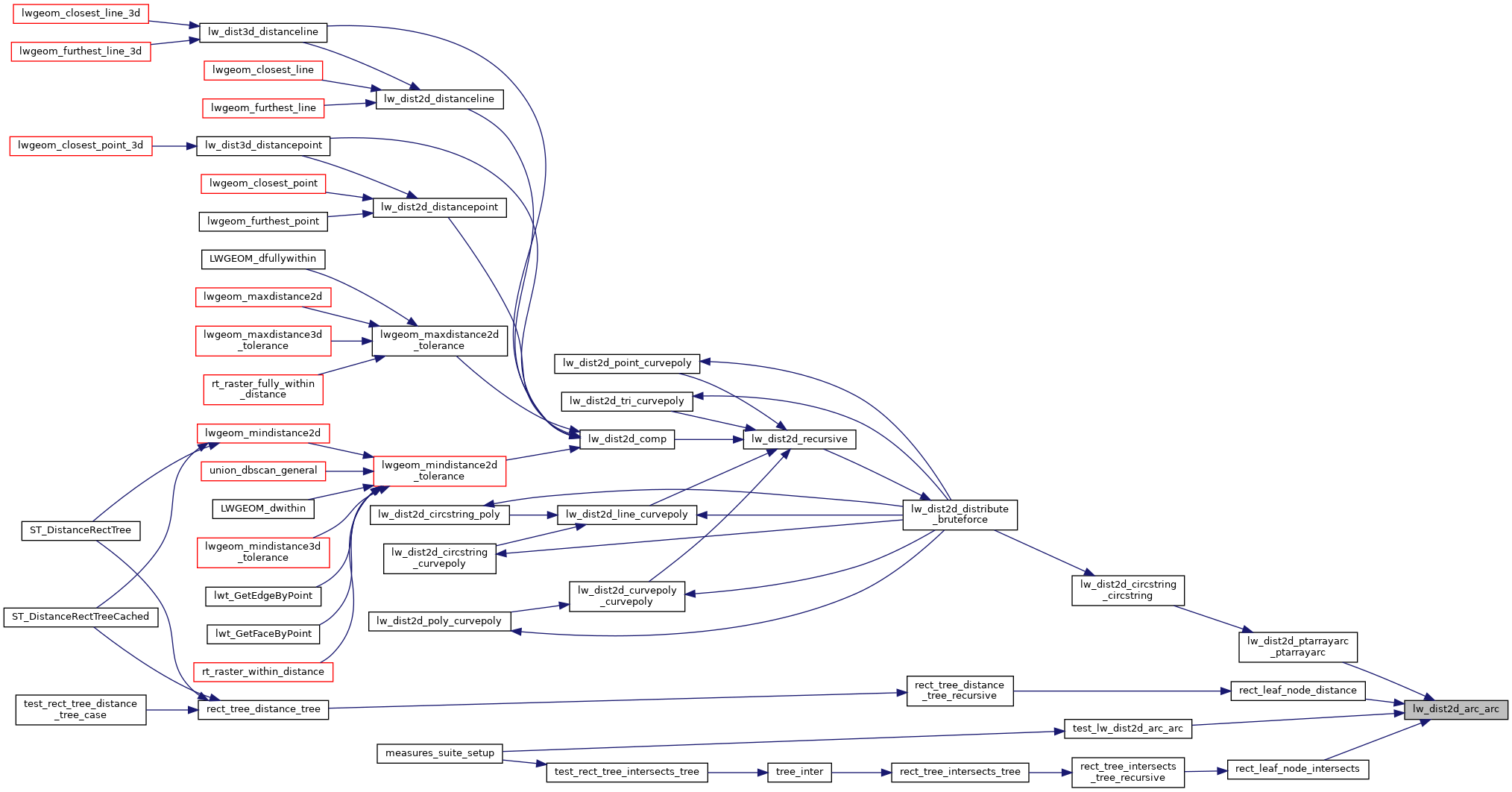
Referenced by lw_dist2d_ptarrayarc_ptarrayarc(), rect_leaf_node_distance(), rect_leaf_node_intersects(), and test_lw_dist2d_arc_arc().

Here is the call graph for this function:

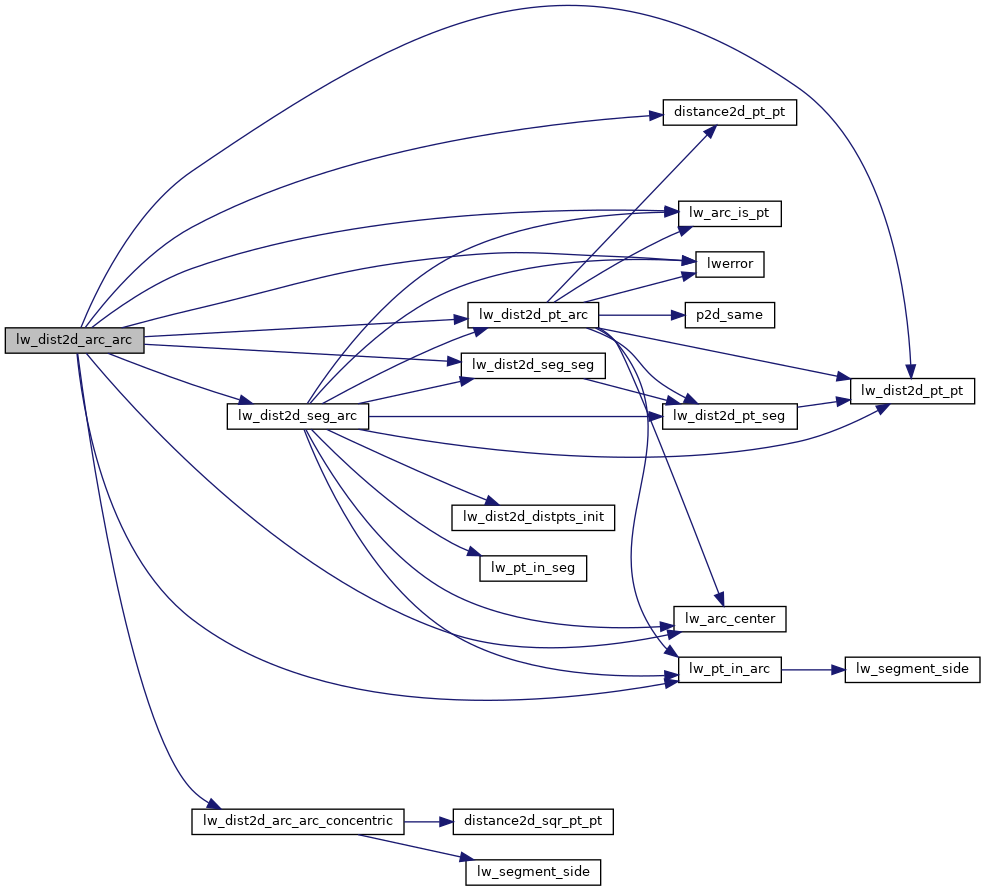
Here is the caller graph for this function: