ST_DelaunayTriangles
Prev  7.14. Geometribearbetning  Next

Name

ST_DelaunayTriangles — Returnerar Delaunay-trianguleringen av hörnen i en geometri.

Synopsis

geometry ST_DelaunayTriangles(geometry g1, float tolerance = 0.0, int4 flags = 0);

Beskrivning

Beräknar Delaunay-trianguleringen av hörnen i indatageometrin. Den valfria toleransen kan användas för att fästa ihop närliggande indatavertikaler, vilket förbättrar robustheten i vissa situationer. Resultatgeometrin avgränsas av den konvexa skrovet av indatapunkterna. Representationen av resultatgeometrin bestäms av flaggkoden:

  • 0 - en GEOMETRYCOLLECTION av triangulära POLYGONER (standard)

  • 1 - en MULTILINESTRING av trianguleringens kanter

  • 2 - En TIN av trianguleringen

Utförs av GEOS-modulen.

Tillgänglighet: 2.1.0

Denna funktion stöder 3d och kommer inte att tappa z-index.

Denna funktion stöder trianglar och triangulerade oregelbundna nätverksytor (TIN).

Exempel

Ursprungliga polygoner

our original geometry
    ST_Union(ST_GeomFromText('POLYGON((175 150, 20 40,
            50 60, 125 100, 175 150))'),
        ST_Buffer(ST_GeomFromText('POINT(110 170)'), 20)
        )

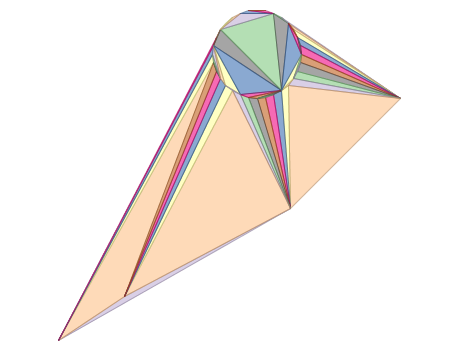
ST_DelaunayTrianglar av 2 polygoner: delaunay-triangelpolygoner varje triangel med tema i olika färger


geometries overlaid multilinestring triangles

SELECT
    ST_DelaunayTriangles(
        ST_Union(ST_GeomFromText('POLYGON((175 150, 20 40,
            50 60, 125 100, 175 150))'),
        ST_Buffer(ST_GeomFromText('POINT(110 170)'), 20)
        ))
     As  dtriag;

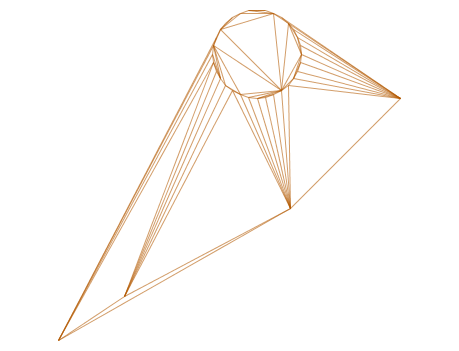
-- delaunay-trianglar som multilinestring

SELECT
    ST_DelaunayTriangles(
        ST_Union(ST_GeomFromText('POLYGON((175 150, 20 40,
            50 60, 125 100, 175 150))'),
        ST_Buffer(ST_GeomFromText('POINT(110 170)'), 20)
        ),0.001,1)
     As  dtriag;

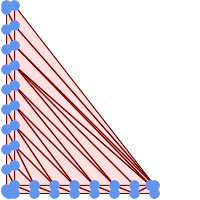
-- delaunay-trianglar med 45 punkter som 55 triangelpolygoner


this produces a table of 42 points that form an L shape

SELECT (ST_DumpPoints(ST_GeomFromText(
'MULTIPOINT(14 14,34 14,54 14,74 14,94 14,114 14,134 14,
150 14,154 14,154 6,134 6,114 6,94 6,74 6,54 6,34 6,
14 6,10 6,8 6,7 7,6 8,6 10,6 30,6 50,6 70,6 90,6 110,6 130,
6 150,6 170,6 190,6 194,14 194,14 174,14 154,14 134,14 114,
14 94,14 74,14 54,14 34,14 14)'))).geom
    INTO TABLE l_shape;

output as individual polygon triangles

SELECT ST_AsText((ST_Dump(geom)).geom) As wkt
FROM ( SELECT ST_DelaunayTriangles(ST_Collect(geom)) As geom
FROM l_shape) As foo;


wkt

POLYGON((6 194,6 190,14 194,6 194))
POLYGON((14 194,6 190,14 174,14 194))
POLYGON((14 194,14 174,154 14,14 194))
POLYGON((154 14,14 174,14 154,154 14))
POLYGON((154 14,14 154,150 14,154 14))
POLYGON((154 14,150 14,154 6,154 14))

Exempel med hörnpunkter med Z-värden.


3D multipoint

SELECT ST_AsText(ST_DelaunayTriangles(ST_GeomFromText(
         'MULTIPOINT Z(14 14 10, 150 14 100,34 6 25, 20 10 150)'))) As wkt;


wkt

GEOMETRYCOLLECTION Z (POLYGON Z ((14 14 10,20 10 150,34 6 25,14 14 10))
 ,POLYGON Z ((14 14 10,34 6 25,150 14 100,14 14 10)))