Name
ST_LargestEmptyCircle — Beräknar den största cirkeln som inte överlappar en geometri.
Synopsis
(geometry, geometry, double precision) ST_LargestEmptyCircle(geometry geom, double precision tolerance=0.0, geometry boundary=POINT EMPTY);
Beskrivning
Finner den största cirkeln som inte överlappar en uppsättning punkt- och linjehinder. (Polygonala geometrier kan inkluderas som hinder, men endast deras begränsningslinjer används) Cirkelns centrum måste ligga innanför en polygonal gräns, vilken som standard är det konvexa skrovet av indatageometrin. Cirkelns centrum är den punkt innanför gränsen som har det längsta avståndet från hindren. Själva cirkeln består av mittpunkten och en närmaste punkt som ligger på ett hinder som bestämmer cirkelns radie.
Cirkelns centrum bestäms med en given noggrannhet som specificeras av en avståndstolerans, med hjälp av en iterativ algoritm. Om noggrannhetsavståndet inte specificeras används en rimlig standard.
Returnerar en post med fält:
-
center- cirkelns mittpunkt -
nearest- en punkt på geometrin som ligger närmast centrum -
radie- cirkelns radie
För att hitta den största tomma cirkeln i det inre av en polygon, se ST_MaximumInscribedCircle.
Tillgänglighet: 3.4.0.
Kräver GEOS >= 3.9.0.
Exempel
SELECT radius,
center,
nearest
FROM ST_LargestEmptyCircle(
'MULTILINESTRING (
(10 100, 60 180, 130 150, 190 160),
(20 50, 70 70, 90 20, 110 40),
(160 30, 100 100, 180 100))');
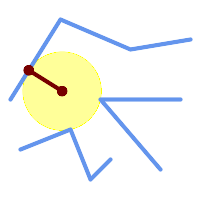
Största tomma cirkel inom en uppsättning linjer.
SELECT radius,
center,
nearest
FROM ST_LargestEmptyCircle(
ST_Collect(
'MULTIPOINT ((70 50), (60 130), (130 150), (80 90))'::geometry,
'POLYGON ((90 190, 10 100, 60 10, 190 40, 120 100, 190 180, 90 190))'::geometry),
0,
'POLYGON ((90 190, 10 100, 60 10, 190 40, 120 100, 190 180, 90 190))'::geometry
);
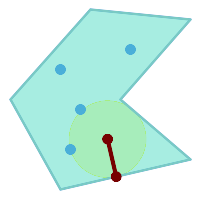
Största tomma cirkel inom en uppsättning punkter, begränsad till att ligga i en polygon. Den begränsande polygongränsen måste inkluderas som ett hinder, samt specificeras som begränsning för cirkelns centrum.